En esta página se recoge información descriptiva de las asignaturas optativas de 8º semestre del Grado en Ingeniería Informática, recogidas en orden alfabético:
Los principales objetivos de la asignatura se resumen en:
Ninguno específico.
Agustín Álvarez Marquina: aalvarez@fi.upm.es
Los contenidos de la asignatura ADW responden a los siguientes objetivos:
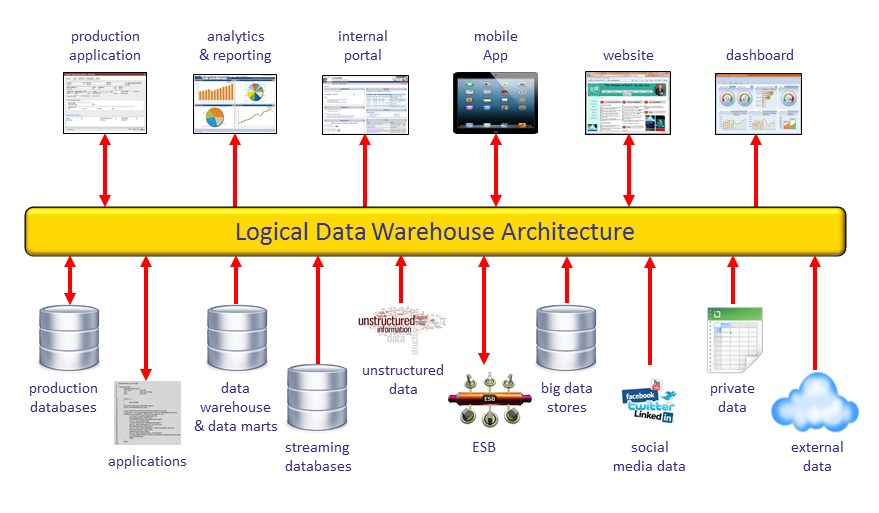
Se plantean durante el curso diversos proyectos prácticos en los que se trabajará extensamente con SQL, MySQL, herramientas ETL (Pentaho) y otras relacionadas con escenarios de Business Intelligence. Se recomienda estar familiarizado con el sistema operativo Linux dado que ello facilita sobre manera el despliegue de los proyectos prácticos. En particular, se va a usar Docker.
A modo de iniciación se recomienda consultar el siguiente enlace: https://www.tutorialspoint.com/dwh/index.htm
Resultan casi imprescindibles los siguientes conocimientos/competencias:
Otro aspecto esencial es que la asistencia a clase es absolutamente recomendable. De hecho, se evalúa explícitamente la participación activa del estudiante de modo que una parte de la nota depende de ello. Recalcar no obstante que la asignatura es optativa por lo que se desaconseja totalmente matricularse a aquellos alumnos que no puedan o no quieran asistir a clase o, por el motivo que sea, no puedan realizar un seguimiento normal de la asignatura.
Santiago Eibe: seibe@fi.upm.es
Supongamos que Alice y Bob estén implementando un sistema informático. Alice se encuentra con un fragmento de código P que quiere reutilizar, pero no está segura de lo que el código hace. Por esto pide a Bob que le diga lo que P calcula (Nota: este programa está escrito en el lenguaje usado por el analizador Interproc; se trata de una lenguaje muy sencillo que cualquier informático con conocimientos de algún lenguaje imperativo puede entender fácilmente):
proc p(a:int) returns (b:int) // rutina
begin
b = a*2;
end
var x:int, y:int; // programa principal que llama p
begin
x = 20;
y = p(x);
end
Es muy fácil entender el resultado del cálculo de P, así que Bob puede contestar a la pregunta en pocos segundos y sin ningún impedimento.
Ahora supongamos que Alice encuentra otro fragmento de código, Q, y, otra vez, quiere usarlo en su sistema. Para ello, pide a Bob que eche un vistazo a Q y le diga lo que calcula (Nota: para los que tengan dudas, "/" es la división entera y "%" es el resto):
proc p(a:int) returns (b:int) // rutina
var c1:int, c2:int, c3:int;
begin
c1 = a / 3;
c2 = a % 3 - 1;
b = c2;
c3 = c1;
while (c3>0) do
b = b + c3 % 3 + 2;
c3 = c3 - 1;
done;
if (c2 > 1) then
b = b + 2;
else
b = b + c2 + 1;
endif;
b = b + c1 * 3;
if (c1 % 3 == 2) then
b = b + c3;
else
b = b + 1;
endif;
end
var x:int, y:int; // programa principal
begin
x = 20;
y = p(x);
end
Es evidente que entender lo que hace Q es mucho más difícil, así que Bob tarda un buen rato para contestar. Sin embargo, el resultado final es que... ¡P y Q calculan exactamente lo mismo!
En general, Bob podrá con cualquier fragmento de código, y encontrará una respuesta para todas las preguntas que Alice le pueda poner. Lo malo es que podría tardar muchísimo (no sería muy difícil producir programas mucho más largos y complejos que sigan calculando la misma función). Por esto los informáticos intentan desarrollar unos programas, que llamaremos analizadores, que realicen el trabajo de Bob tardando mucho menos y con un mayor nivel de fiabilidad.
Lo que pasa es que ni siquiera el analizador más potente podrá contestar a todas las preguntas de Alice: siempre habrá un programa para el que no sabrá dar una respuesta (en este caso, que el valor final de "y" es 40).
En este curso vamos a entender por qué pasa esto.
Damiano Zanardini: damiano@fi.upm.es
El término Fotografía Computacional se refiere a las diferentes técnicas que extienden las capacidades de la fotografía digital.
En la fase de adquisición esto puede suponer modificar el diseño de una cámara tradicional para capturar información adicional (por ejemplo, distancia a la cámara a través del grado de desenfoque). En la fase de manipulación o procesado, podemos destacar aplicaciones donde diferentes imágenes se combinan en panoramas o imágenes de alto rango dinámido (HDR). Otros ejemplos incluyen la combinación de fotografías con diferente iluminación (flash/no flash) o la fusión de partes de diferentes fotografías en una única imagen. En todas estas técnicas el resultado es una imagen ordinaria, pero una que no podría haberse obtenido con una cámara tradicional.
Durante este curso, siguiendo el hilo argumental del proceso fotográfico se presentarán varias de las aplicaciones que pueden aparecer en la formación, captura y procesado de una imagen digital. En cada caso se presentará el problema matemático subyacente y los algoritmos para resolverlo, alternando esas explicaciones con su implementación en el laboratorio (usando MATLAB).
Fundamentos de álgebra lineal, conocimientos de MATLAB, interés por la fotografía.
Antonio Tabernero Galán: ant@fi.upm.es
La representación de objetos tridimensionales en dos dimensiones ha sido objeto de estudio durante mucho tiempo: desde el Renacimiento, que los pintores desarrollaron técnicas matemáticas que lo elevaron a nivel de ciencia, hasta nuestros días con los motores gráficos actuales. En este curso veremos un motor gráfico, OpenGL, sobre el que aprenderemos de forma introductoria a programar con esta librería, y nos centraremos en las matemáticas que hay debajo de ese motor, enfocándonos sobre todo en los aspectos geométricos. Ello nos obligará a repasar el Álgebra Lineal, pero también a introducirnos en los espacios afín y proyectivo, y sus transformaciones.
Jonatan Sánchez Hernández: jonatan.sanchez@fi.upm.es
Image understanding, which is based on the results of image processing and analysis, attempts to interpret the meaning of an image at a high level in order to provide semantic information closely related to human thought, to help make decisions and to guide actions according to the understanding of the scenes. This course is an introduction to the fundamental concepts in image understanding. A variety of interesting vision problems and techniques will be studied. Specifically, the course will cover image characteristics, feature extraction, image classification, object recognition.
Previous courses:
Other recommended knowledge:
Ángel García Pedrero: agpedrero@fi.upm.es
La asignatura de Ingeniería de Protocolos de Comunicaciones tiene como objetivo que el alumno conozca, en primer lugar, las técnicas de descripción formal utilizadas para especificar protocolos de comunicaciones como paso previo para su posterior implementación y sus ventajas para la generación automática de código fuente. El alumno utilizará herramientas como SDL (Specification and Description Language) ampliamente utilizadas en la industria en la descripcion formal de protocolos.
En segundo lugar, el alumno será capaz de identificar y manejar las interfaces de programación de software de comunicaciones más habituales hoy en día como los Sockets de Berkeley, Windows Sockets, Sockets en Java, en Python o Android.
Por último, el alumno será capaz de comprender las técnicas de implementación de aplicaciones distribuidas utilizando las diferentes interfaces de programación así como analizar el rendimiento de las soluciones planteadas. En definitiva, el alumno será capaz de diseñar e implementar el software de comunicaciones en la mayoría de las aplicaciones distribuidas
Conocimientos de programación, Java, C, C++
Luis Mengual Galán lmengual@fi.upm.es
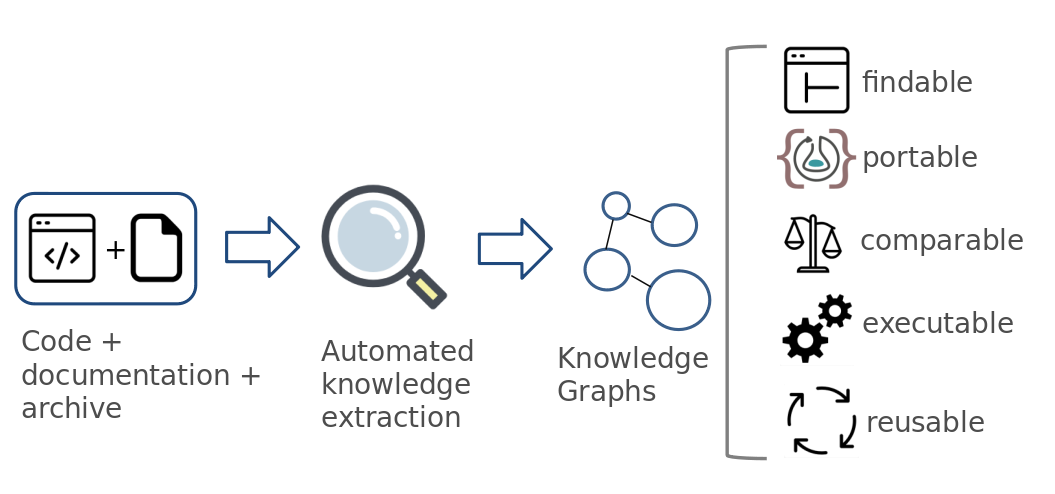
El objetivo de este curso es que los estudiantes aprendan los fundamentos de la IA en la Ingeniería de Software Científico, con un enfoque especial en aplicaciones del mundo real. El curso incluirá conocimientos teóricos y metodológicos sobre técnicas avanzadas de IA diseñadas para ayudar a la reproducibilidad y reutilización de software, datos y sus metadatos en el ámbito de investigación, con aplicaciones en industria.
En concreto, el curso abordará la importancia de la reproducibilidad en ciencia, enfoques existentes para administrar, empaquetar y entregar un producto de investigación, la planificación y ejecución en paralelo de experimentos computacionales complejos, la creación de grafos de conocimiento para facilitar la búsqueda y la configuración de software científico; así como técnicas de aprendizaje automático para identificar similitudes entre software. La asignatura presentará aplicaciones que combinan todo lo anterior para facilitar la integración y comprensión de datos y software científicos.
Inteligencia artificial, Web semántica, Datos enlazados y grafos de conocimiento, Ingeniería de software
La Minería de Datos trata de construir sistemas informáticos cuando no existe experiencia humana o cuando no es fácilmente explicable. Así, los datos se transforman en conocimiento. Entre las muchas aplicaciones exitosas pueden citarse el reconocimiento del habla o de texto manuscrito, navegación autónoma de robots, recuperación de información documental, filtrado cooperativo, sistemas de diagnóstico, análisis de microarrays de ADN, etc.
Este curso expone varios métodos de Minería de Datos desde el punto de vista práctico. El objetivo es enfrentarse a un conjunto de datos sobre los que construir modelos clasificatorios con la ayuda del software WEKA.
Probabilidades y estadística I
Pedro Larrañaga: pedro.larranaga@fi.upm.es
With the advent in the last decade of streaming platforms like Netflix, Youtube, HBO, and Amazon Prime Video, more than 80% of Internet traffic corresponds to multimedia content (and more specifically, to video content). This makes it necessary to compress this kind of content more and more.
The "Multimedia" course aims to provide the knowledge needed to identify different types of multimedia content, to understand the techniques used to compress and encode audiovisual contents, and to learn about the main standards for image, video and audio coding, as well as for multimedia systems.
We will study how a 90 minute long Full HD film can be compressed into a less than 1 GB file, when the raw video would produce a 1 TB file. With this in mind, we will study how some of the most well-known standards for multimedia content work, such as JPEG for pictures or MP3 for audio.
No specific requirements are needed.
Antonio Jesús Díaz Honrrubia: antoniojesus.diaz@upm.es
The implementation of applications or services with a strong presence on the Internet, such as social network applications, present great challenges: design and programming of back-ends (services) that support the popularization of the application, and design and programming of front-ends (mobile applications and web applications) with a good user experience, elegant interfaces, and efficient access to the back-end.
The course focuses on the design and programming of the back-end of this type of applications. We list some of the fundamental requirements:
The course delves into the Erlang/OTP ecosystem and the Elixir language. Elixir takes advantage of the Erlang virtual machine, well known for its ability to run low-latency, distributed, and fault tolerant systems. Some examples of applications and systems where these languages have been used are: WhatsApp, Cabify, bet365, Nintendo Switch multi-user online gaming or RabbitMQ.
Prerrequisites: "Concurrencia" and "Sistemas Operativos". Also recommended: take some contact with functional programming concepts.
Ángel Herranz: aherranz@fi.upm.es
En la asignatura se realiza una introducción a la robótica móvil y a la visión por computador. En concreto, los estudiantes estudiarán sistemas de control y navegación, la formación de imágenes, la segmentación de imágenes y el reconocimiento de objetos planos. Con los conocimientos adquiridos, los alumnos realizarán una práctica con un robot real. En esta práctica el robot tiene que usar una cámara de vídeo para identificar una línea pintada en el suelo, seguir esta línea detectando bifurcaciones y usar la identificación de símbolos en el suelo para elegir entre las posibles salidas.
La práctica de la asignatura tiene una carga importante de programación en Python, así se recomienda la asignatura para alumnos con confianza en sus habilidades de programación. También se recomienda haber cursado la asignatura de Inteligencia Artificial y Reconocimiento de Formas.
Nik Swoboda: nswoboda@fi.upm.es
Los sistemas dinámicos y el concepto de caos aparecen de manera natural en muchos procesos que siguen leyes deterministas, o estocásticas, por eso son una herramienta fundamental para simular y estudiar la evolución de estos procesos. En el primer tema se hace un análisis detallado de la familia logística que surge como uno de los modelos más sencillos de dinámicas de poblaciones y en la que aparece la gama completa de posibles comportamientos de sistemas dinámicos unidimensionales, desde los más simples hasta los caóticos. También se estudian los sistemas dinámicos bidimensionales y complejos que dan origen a los conjuntos de Julia y Mandelbrot. Algunos de estos procesos evolucionan hacia atractores extraños y poseen una estructura fractal. El alumno aprenderá a generar los fractales autosemejantes como el triángulo de Sierpinski, la curva de Koch y en general a cualquier fractal generado por un sistema de funciones iteradas cuyo atractor es precisamente el fractal. Esta es la base para la simulación y compresión fractal de imágenes.
La asignatura se desarrolla toda en laboratorio y el alumno implementa los algoritmos y experimenta los conceptos a través de prácticas en Python, Maple o Matlab.
No se definen.
M. Del Carmen Escribano Iglesias: cescribano@fi.upm.es
Al inicio de la asignatura introducimos los conceptos básicos de teoría de la información que necesitamos para después estudiar dos problemas: la compresión de datos y la corrección de errores.
En la primera parte de la asignatura partimos del concepto de fuente de información y de una medida de la información para comprender los límites teóricos de la compresión de datos. Veremos distintos algoritmos para mejorar la codificación de cualquier archivo, así como la forma de alcanzar una codificación (compresión) óptima.
En la segunda parte de la asignatura aprenderemos a calcular la capacidad de un canal de comunicación. El alumno podrá entonces determinar la tasa máxima de error que cualquier código es capaz corregir de forma teórica. Estudiaremos entonces los códigos detectores y correctores de errores, las propiedades que debe cumplir un buen código corrector, y revisaremos los métodos clásicos de detección y corrección de errores basados en códigos lineales. Finalmente presentamos las técnicas modernas de corrección de errores y su implementación óptima, estudiaremos los distintos algoritmos utilizamos para la codificación y decodificación con dichos códigos, sus optimizaciones, y los métodos para la construcción de buenos códigos correctores.
El objetivo final de la asignatura es introducir al alumno en las técnicas modernas (algoritmos) utilizadas en la detección y corrección de errores, y que hoy día forman parte de estándares en tecnologías tan conocidas como Wi-Fi, Wimax, o DVB, entre otras.
Álgebra Lineal
Jesús Martínez Mateo: jmartinez@fi.upm.es
